YOLO是“You Only Look Once”的缩写，YOLO将物体检测作为回归问题求解，是一个对象检测算法的名字，这是Redmon等人在2016年的一篇研究论文中命名的。

20191020111518954

本篇文章会一步一步搭建起yolov3的神经网络，详细内容会具体分析。

YOLO介绍

目标检测（object detection）是一个因近年来深度学习的发展而受益颇多的领域，近年来，人们开发了多种目标检测算法，其中包括YOLO、SSD、Mask-RCNN和RetinaNet。此篇文章使用PyTorch并基于YOLO v3来实现一个目标检测器，这是一种速度更快的目标检测算法。

YOLO是“You Only Look Once”的缩写，YOLO将物体检测作为回归问题求解，是一个对象检测算法的名字，这是Redmon等人在2016年的一篇研究论文中命名的：

Redmon J , Divvala S , Girshick R , et al. You Only Look Once: Unified, Real-Time Object Detection[J]. 2015.

YOLO结构

以下为yolo的整体结构：

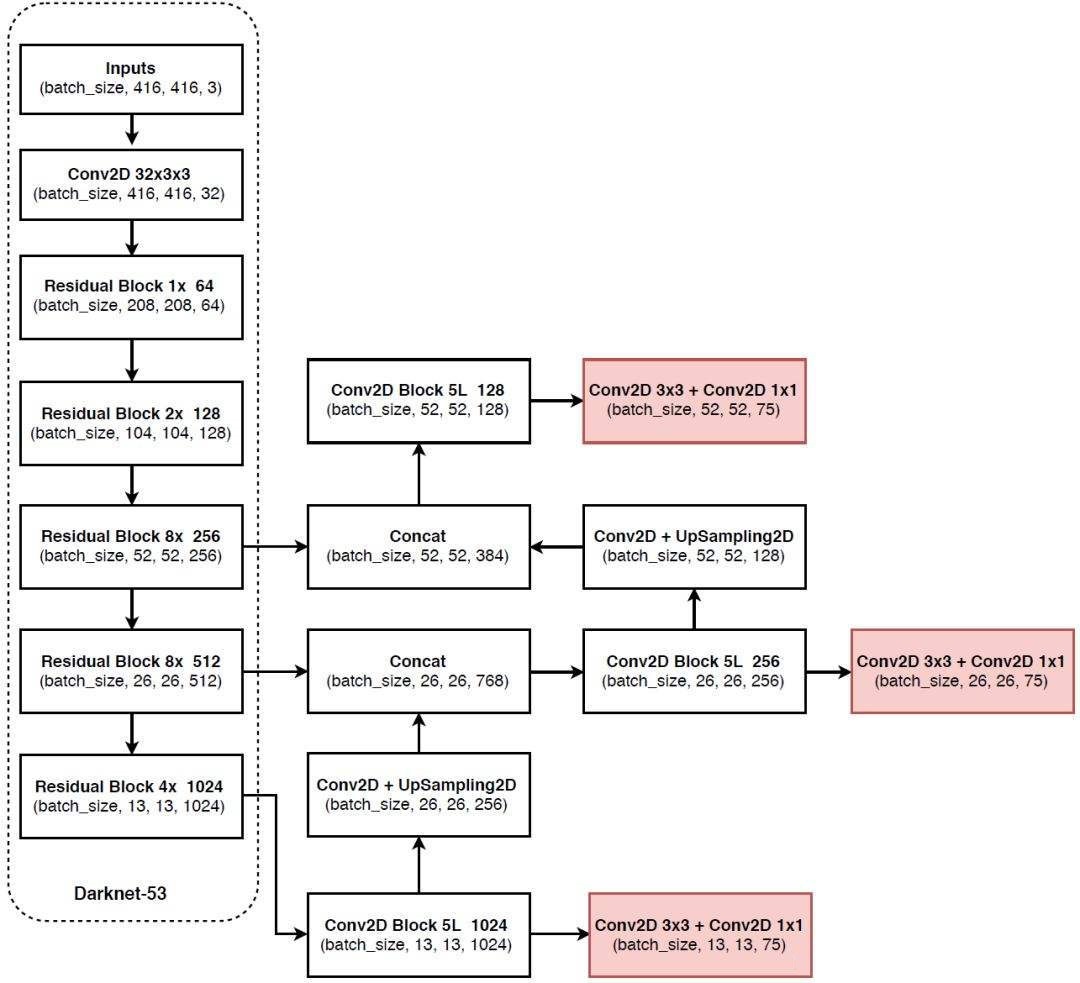
20191020111518954

这张图分成两部分，左边虚线框起来的是主干特征提取部分。

主干特征提取

这部分称作Darknet-53，主干特征提取顾名思义，用来提取图片的特征。

输入是需要一张$416 416 3$大小的图片，然后是不断卷积的过程，如果仔细看会发现图片的高和宽不断被压缩，通道数却不断扩张，这是一个下采样过程。

经过下采样之后，会获得特征层（用来表述图片的特征），下图是我们需要的特征层。

2019

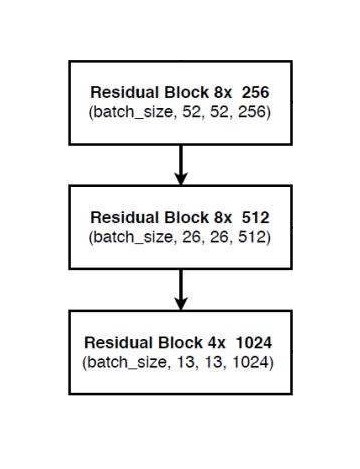
由此可见保留下来的特征层为：$5252256$、$2626512$、$13131024$三种尺寸，这三种特征层是即将传入右边的部分。

1437686-20200102124439991-778619867

每个特征图可以看作一个“条目”，因为一个“条目”有一些信息，如下图所示：

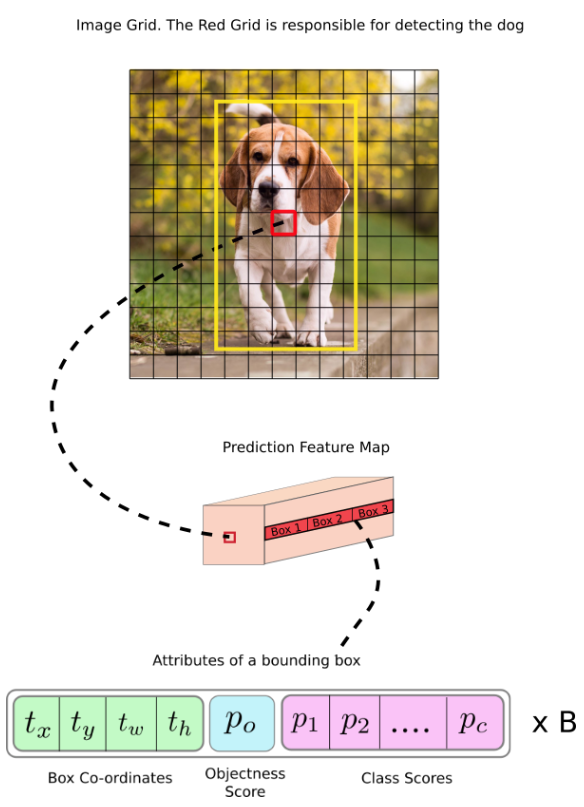
1437686-20191230192708001-430020660

其他部分

这里的其他部分泛指右边部分的网络。

经过主干特征提取后，我们获得了三种尺寸的特征层，分别对三种尺寸的特征层处理。

处理$13131024$特征层

首先说一下$13131024$特征层的处理：

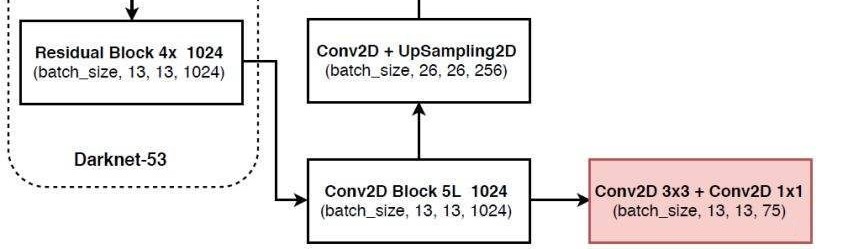
10201

可以看到$13131024$特征层经过了5次卷积后传到了两个方向。

右边的粉色部分是分类预测和回归预测，其实就是两次卷积，最后会获得$131375$大小的，再经过一个分解变成$1313325$，即$13133(20 + 1 + 4)$，这个过程其实就是化成$1313$的网格，每个网格有3个预测出的*先验框，接下来会根据判断属于那种框的尺寸。

之所以会把25分成三部分，其实就gailv是20个物体分类，由于使用voc数据集，所以会有20个，coco训练集会出现80个，简单来讲20个置信度（属于哪个类的概率）会分类属于哪个类；1是指是否有物体；4是对框的调整。

注意$13131024$特征层还有一个传递方向，这时需要一个上采样，也就是扩增长宽，减小通道数。经过上采样之后会和$2626512$特征层进行堆叠（增加通道数）。

处理$2626512$特征层

$2626512$特征层在和经过上采样的$13131024$特征层进行堆叠后，会形成一个新的“特征金字塔”，当然这个特征金字塔还会继续堆叠。

0111

后面的部分就一样了，再5次卷积，在最后进行分类预测和回归预测，会出现相同操作。

与此同时会把5次卷积后继续向上传递，并有个上采样。

$5252256$特征层同样如此就不再赘述。

输出结果：

$t_x$和$t_y$是被检测物体的中心位置，$t_w$和$t_h$是方框的尺寸，$p_0$是物体置信度，代表了这个区域内有物体的概率，$p_1->p_c$是分类置信度，哪类概率高，就属于什么物体。最后还有个B，这个是锚框个数，说明了这个区域可以最多检测出B个物体。

Anchor Boxes

有的翻译成锚框，有的翻译成先验框，这里我就叫它锚框了。

YOLO不能直接预测边界框的宽度和高度，这会导致训练过程中出现不稳定的变化。大多数现代目标检测器会预测对数空间转换，或者只是偏移到称为锚点的预定义默认锚框。YOLO-v3具有三个锚点，可在每个细胞单元格上预测三个边界框。

那么真正的方框是怎么预测出的？先看下面的公式：

前两个公式是预测中心点，经过$\sigma()$函数后就会稳定在0和1之间。$c_x$和$c_y$是第几个方框，例如上图中红色框的这两值都是6。

后面两个公式预测宽度，$p_w$和$p_h$是锚框的尺寸，直接乘就可以。

还没有完，这只完成了一半，接着看：

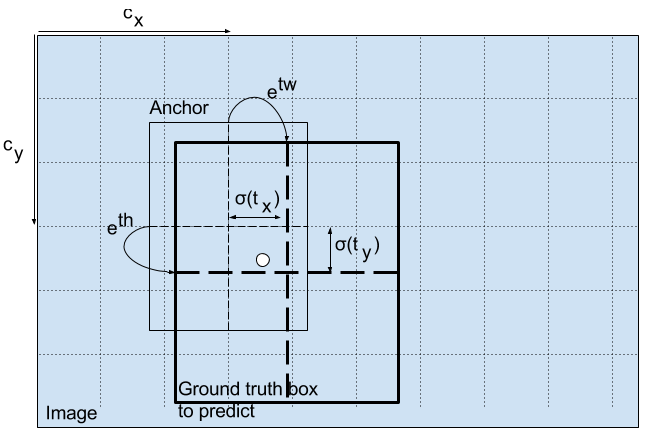
1437686-20200102121153977-382469172

中心点需要还乘上对应的网格宽度，方框需要带入e指数中。

补一张更漂亮的图。

v2-fb8b964727ccfea93345ba1361c4c8a3_720w

YOLO预测原理

YOLO将图片分成了3种检测，检测的区别是按照分割区域的大小。

首先输入图片的大小要定下为$416*416$大小，如果不合适就要补上缺失部分，目的就是防止失真。

将图片分别分成$5252$、$2626$、$13*13$、三种尺寸的网格，针对的识别三种尺寸，也就对应上了上部分的三种输出结果。

每个输出结果的维度为(N, 75 * 3, x, x)，x为尺寸分别对应52、26、13三种，N代表样本数，75 * 3这个数在上面提过了就不再多说。

最后的最终的预测结构后还要进行得分排序与非极大抑制筛选。

用$77$来举例（我只找到$77$的例子，我又懒得去做$1313$的图），下面将一幅图分成$77$网格，共49部分。

8694a4c27d1ed21bc6ed15f6c38952c250da3fee

对于每个网格点，都会预测一个边界框和与每个类别（汽车，行人，交通信号灯等）相对应的概率，每个网络点负责一个区域的检测。

程序

首先搭建DarkNet大概框架：

1
2
3
class DarkNet(nn.Module):
    def __init__(self, layers):
        super(DarkNet, self).__init__()

DarkNet继承了pytorch中的模型，目的使用一些相同的框架函数。

初始的卷积层

继续根据整体结构来加入每一层，首先卷积层：

1
2
3
4
5
6
# 设置卷积核个数，也是卷积后的通道数
self.inplanes = 32
# 大概配置参数是：
# 输入通道数、输出通道数（卷积核个数）、卷积核尺寸、步长填充、是否加入偏置
# 此时下面的配置是same卷积，没有破坏图像原本的大小
self.conv1 = nn.Conv2d(3, self.inplanes, kernel_size=3, stride=1, padding=1, bias=False)

标准化和激活函数：

注意：这里使用的是LeakyReLU，这样好处是，负数区域还存在值，同时也有斜率。

1
2
3
4
# BatchNorm标准化，加速收敛速度及稳定性的算法
self.bn1 = nn.BatchNorm2d(self.inplanes)
# 设置激活函数
self.relu1 = nn.LeakyReLU(0.1)

以上操作建立了一个卷积层，最后生成的维度为：(N, 416, 416, 32)

残差块

先制做出残差块的函数，返回值是一个残差块：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def _make_layer(self, planes, blocks):
    """
    制作一个结构块
    :param planes: 是个列表，第一位置是输入通道数，第二位置是输出通道数
    :param blocks: 残差块堆叠个数
    :return:
    """
    layers = []
    # 下采样，步长为2，卷积核大小为3，填充为1
    # 这样长宽就可以压缩
    layers.append(("ds_conv", nn.Conv2d(self.inplanes, planes[1], kernel_size=3,
                            stride=2, padding=1, bias=False)))

    # BatchNorm标准化
    layers.append(("ds_bn", nn.BatchNorm2d(planes[1])))
    # 设置激活函数
    layers.append(("ds_relu", nn.LeakyReLU(0.1)))

    # 加入darknet模块
    self.inplanes = planes[1]

    # 堆叠残差块
    for i in range(0, blocks):
        # 添加一个网络
        # layers是个列表，里面元素是元组，元组元素是字符串和BasicBlock网络块
        layers.append(("residual_{}".format(i), BasicBlock(self.inplanes, planes)))

    # 打包网络
    return nn.Sequential(OrderedDict(layers))

OrderedDict是有序字典，虽然平常不常用，但在这里使用是最合适的，记得导入包：

1
from collections import OrderedDict

最核心的部分是BasicBlock类，这里是残差网络相加的地方：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

# 基本的darknet块（残差块的核心）
class BasicBlock(nn.Module):
    def __init__(self, inplanes, planes):
        """
        残差块
        :param inplanes:
        :param planes: 下采样部分
        """
        super(BasicBlock, self).__init__()

        # 定义了两组卷积操作

        # 最开始是卷积核形状为1的卷积
        # 目的是下降通道数
        self.conv1 = nn.Conv2d(inplanes, planes[0], kernel_size=1,
                               stride=1, padding=0, bias=False)
        # BatchNorm标准化
        self.bn1 = nn.BatchNorm2d(planes[0])
        # 设置激活函数
        self.relu1 = nn.LeakyReLU(0.1)
        
        # 为了保证残差成功，必须使用same卷积
        # 这里还将通道数提升了
        self.conv2 = nn.Conv2d(planes[0], planes[1], kernel_size=3,
                               stride=1, padding=1, bias=False)
        # BatchNorm标准化
        self.bn2 = nn.BatchNorm2d(planes[1])
        # 设置激活函数
        self.relu2 = nn.LeakyReLU(0.1)

    def forward(self, x):
        # 保存残差”边“
        residual = x

        # 传统艺能
        
        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu1(out)

        out = self.conv2(out)
        out = self.bn2(out)
        out = self.relu2(out)

        # 网络最后加上残差边
        out += residual
        return out

由于里面先进行1卷积，再3卷积，这样可以减少参数量，

初始化剩下的东西：

1
2
3
4
5
6
7
8
9
10
11
   # 
self.layers_out_filters = [64, 128, 256, 512, 1024]

   # 进行权值初始化
   for m in self.modules():
       if isinstance(m, nn.Conv2d):
           n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
           m.weight.data.normal_(0, math.sqrt(2. / n))
       elif isinstance(m, nn.BatchNorm2d):
           m.weight.data.fill_(1)
           m.bias.data.zero_()

前向传播

前向传播的时候我们需要返回三个尺寸的特征图，所以需要这样写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def forward(self, x):
    """
    前向传播
    :param x: 输入图
    :return: 三个特征图
    """

    # 传统艺能
    x = self.conv1(x)
    x = self.bn1(x)
    x = self.relu1(x)

    x = self.layer1(x)
    x = self.layer2(x)

    # 第一特征图
    out3 = self.layer3(x)
    # 第二特征图
    out4 = self.layer4(out3)
    # 第三特征图
    out5 = self.layer5(out4)

    return out3, out4, out5

从特征获取预测结果

特征图出来了，但我们需要将特征图转换成最终结果。

在放代码之前，自定义一套卷积，这是方便后面快速使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def conv2d(filter_in, filter_out, kernel_size):
    """
    私自定义的卷积
    :param filter_in: 输入通道数
    :param filter_out: 输出通道数
    :param kernel_size: 卷积核尺寸
    :return:
    """
    pad = (kernel_size - 1) // 2 if kernel_size else 0
    return nn.Sequential(OrderedDict([
        ("conv", nn.Conv2d(filter_in, filter_out, kernel_size=kernel_size, stride=1, padding=pad, bias=False)),
        ("bn", nn.BatchNorm2d(filter_out)),
        ("relu", nn.LeakyReLU(0.1)),
    ]))

这个卷积相当于一套完整的卷积层，但官方这里没有使用残差网络，这有点让我感到疑惑，因为我担心这样会不会影响整个网络前部分的梯度计算。

主体部分的初始化

因为是主体部分，所以首先创建yolo主体：

1
2
3
4
5
6
7
8
class YoloBody(nn.Module):
    def __init__(self, config):
        """
        yolo主体
        :param config:
        """
        super(YoloBody, self).__init__()
        self.config = config

然后获取已经创建好的网络（也就是上面的程序）：

1
2
3
4
5
# 获取darknet53堆叠网络
self.backbone = darknet53(None)

# 获取输出通道数
out_filters = self.backbone.layers_out_filters

接下来就是$13*13$特征层的提取：

1
2
3
4
5
6
# last_layer0
# 此值为75
final_out_filter0 = len(config["yolo"]["anchors"][0]) * (5 + config["yolo"]["classes"])
# 5次卷积+2次卷积
self.last_layer0 = make_last_layers([512, 1024], out_filters[-1], final_out_filter0)

现在详细说一下final_out_filter0这个变量特点，此变量分两部分，两部分相乘才出结果。len(config["yolo"]["anchors"][0])是先验框个数，我们使用了3个，所以此结果是3；(5 + config["yolo"]["classes"])这个是$20 + 1 + 4$，也就是25。最终结果就是$(20+1+4)*3=75$。

这个时候有个make_last_layers函数，这就是5次卷积和最后结果卷积。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def make_last_layers(filters_list, in_filters, out_filter):
    """
    5次卷积+2次卷积
    :param filters_list:中间过渡通道数
    :param in_filters: 输入通道数
    :param out_filter: 输出通道数
    :return: 5次卷积+2次卷积的模型
    """
    m = nn.ModuleList([
        # 1*1卷积调整通道（降低通道数）
        conv2d(in_filters, filters_list[0], 1),
        # 3*3卷积提取特征
        conv2d(filters_list[0], filters_list[1], 3),
        # 1*1卷积调整通道（降低通道数）
        conv2d(filters_list[1], filters_list[0], 1),
        # 3*3卷积提取特征
        conv2d(filters_list[0], filters_list[1], 3),
        # 1*1卷积调整通道
        conv2d(filters_list[1], filters_list[0], 1),

        # 接下来两此卷积用来分类预测和回归预测
        conv2d(filters_list[0], filters_list[1], 3),
        nn.Conv2d(filters_list[1], out_filter, kernel_size=1,
                                        stride=1, padding=0, bias=True)
    ])
    return m

$1*1$卷积是很有效减少通道数，从而减少参数，这对电脑减轻了不小负担。

接下来是$13*13$特征层的提取：

1
2
3
4
5
6
7
8
9
# embedding1
# 此值为75
final_out_filter1 = len(config["yolo"]["anchors"][1]) * (5 + config["yolo"]["classes"])
# 1*1卷积调整通道数（从512调节成256通道）
self.last_layer1_conv = conv2d(512, 256, 1)
# 上采样
self.last_layer1_upsample = nn.Upsample(scale_factor=2, mode='nearest')
# 5次卷积+2次卷积
self.last_layer1 = make_last_layers([256, 512], out_filters[-2] + 256, final_out_filter1)

在使用上采样之前需要用$1*1$卷积核来调整通道，这样可以保证接下来上采样时通道一致。

由于使用上采样，所以我们需要上采样函数，幸运的是pytorch提供了上采样，所以我们免去了这个过程。

最后就是剩下特征层，也是同样道理：

1
2
3
4
5
6
7
8
9
# embedding2
# 此值为75
final_out_filter2 = len(config["yolo"]["anchors"][2]) * (5 + config["yolo"]["classes"])
# 1*1卷积调整通道数（从256调节成128通道）
self.last_layer2_conv = conv2d(256, 128, 1)
# 上采样
self.last_layer2_upsample = nn.Upsample(scale_factor=2, mode='nearest')
# 5次卷积+2次卷积
self.last_layer2 = make_last_layers([128, 256], out_filters[-3] + 128, final_out_filter2)

前向传播

看到这里，所有初始化都完成了，也就是网络结构部分完成了，剩下就是其他的代码，就比如前向传播的整体还没写。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def forward(self, x):
    """
    前向传播
    :param x: 输入
    :return:
    """

    # 函数中定义函数
    def _branch(last_layer, layer_in):
        """
        分开卷积过程
        :param last_layer: 上一层结果
        :param layer_in:会存入卷积过程的结果并会返回出去
        :return: out_branch是最后结果
        """
        for i, e in enumerate(last_layer):
            layer_in = e(layer_in)
            if i == 4:
                # 第五次卷积的时候取出来
                out_branch = layer_in
        return layer_in, out_branch

没错，直接套娃就可以，我挺喜欢这样写，因为这样写可以让整个函数在另一个函数周期里，外函数“死亡”时，里面的函数也会“死亡”。之所以定义这个函数是把第五次卷积结果拿出来，因为需要上采样传递给其他层。

继续写，在DarkNet中我们可以获得到三种特征图。

1
2
# 获取三种特征图
x2, x1, x0 = self.backbone(x)

现在可以正常正向传播了，首先第一套特征图：

1
2
3
# 5次卷积+2次卷积
# 直接可以得到卷积神经网络结果
out0, out0_branch = _branch(self.last_layer0, x0)

第二套特征图使用计算之前，需要调整通道数、上采样、堆叠：

1
2
3
4
5
6
7
8
9
# 1*1卷积调整通道数（从512调节成256通道）
x1_in = self.last_layer1_conv(out0_branch)
# 上采样
x1_in = self.last_layer1_upsample(x1_in)
# 堆叠
x1_in = torch.cat([x1_in, x1], 1)
# 5次卷积+2次卷积
# 直接可以得到卷积神经网络结果
out1, out1_branch = _branch(self.last_layer1, x1_in)

第三套同样如此：

1
2
3
4
5
6
7
8
9
# 1*1卷积调整通道数（从256调节成128通道）
x2_in = self.last_layer2_conv(out1_branch)
# 上采样
x2_in = self.last_layer2_upsample(x2_in)
# 堆叠
x2_in = torch.cat([x2_in, x2], 1)
# 5次卷积+2次卷积
# 直接可以得到卷积神经网络结果
out2, _ = _branch(self.last_layer2, x2_in)

最后直接输出：

1
return out0, out1, out2

以上我们的网络就搭建完毕了，但还缺少解码部分以及损失函数，所以继续写吧。

解码

将解码也定义一个层，这样就方便后续的处理：

1
2
3
4
5
6
7
8
9
class DecodeBox(nn.Module):
    def __init__(self, anchors, num_classes, img_size):
        super(DecodeBox, self).__init__()
        self.anchors = anchors
        self.num_anchors = len(anchors)
        self.num_classes = num_classes
        self.bbox_attrs = 5 + num_classes
        # 保存图像大小
        self.img_size = img_size

前向传播部分：

1
2
3
4
5
6
7
8
9
10
11
def forward(self, input):

    # 此时的形状是（N, 3*(20+5), size, size）

    # 获取图片数量（N,）
    batch_size = input.size(0)

    # 获取图片几行网格
    input_height = input.size(2)
    # 获取图片几列网格
    input_width = input.size(3)

当然还没完，我们还要获得图片步长，也就是图片每个网格内有多少像素点（感受野）：

1
2
3
4
5
# 计算步长
# 每个网格内有多少像素点
# 图片尺寸 / 每个网格大小
stride_h = self.img_size[1] / input_height
stride_w = self.img_size[0] / input_width

我们之前定义了三种先验框，所以注意最开始的先验框的单位是像素，我们需要将这个改变成根据步长的百分比，也就是归一到特征层上：

1
2
# 归一到特征层上
scaled_anchors = [(anchor_width / stride_w, anchor_height / stride_h) for anchor_width, anchor_height in self.anchors]

因为有三套先验框，所以这个循环会执行三次。

还需要通道转换，.permute(0, 1, 3, 4, 2).contiguous()：

1
2
3
# （N, 3*(20+5), size, size）->（N, 3 , size, size, 20+5）
prediction = input.view(batch_size, self.num_anchors,
                        self.bbox_attrs, input_height, input_width).permute(0, 1, 3, 4, 2).contiguous()

处理一下先验框的中心参数，怕是遇到负数，所以使用sigmoid()函数过滤一下，这样百分百是正数且不会大于1：

1
2
3
# 先验框的中心位置的调整参数
x = torch.sigmoid(prediction[..., 0])
y = torch.sigmoid(prediction[..., 1])

还有宽高参数：

1
2
3
# 先验框的宽高调整参数
w = prediction[..., 2]  # Width
h = prediction[..., 3]  # Height

以及物体置信度和种类置信度，听说在之前yolo使用的是softmax()函数，这样就会产生独立事件，有时会出bug，sigmoid()可以解决这个问题：

1
2
3
4
# 获得置信度，是否有物体
conf = torch.sigmoid(prediction[..., 4])
# 获得种类置信度
pred_cls = torch.sigmoid(prediction[..., 5:])

先验框问题解决了，接下来就生成出来，根据网格左上角生成中心：

1
2
3
# 生成网格，先验框中心，网格左上角
grid_x = torch.linspace(0, input_width - 1, input_width).repeat(input_width, 1).repeat(batch_size * self.num_anchors, 1, 1).view(x.shape).type(FloatTensor)
grid_y = torch.linspace(0, input_height - 1, input_height).repeat(input_height, 1).t().repeat(batch_size * self.num_anchors, 1, 1).view(y.shape).type(FloatTensor)

也就是从网格的左上角，每隔size单位生成一个，形状是（N, 3, size, size）

再生成先验框的宽和高，根据自己设定的原始先验框：

1
2
3
4
5
# 生成先验框的宽高
anchor_w = FloatTensor(scaled_anchors).index_select(1, LongTensor([0]))
anchor_h = FloatTensor(scaled_anchors).index_select(1, LongTensor([1]))
anchor_w = anchor_w.repeat(batch_size, 1).repeat(1, 1, input_height * input_width).view(w.shape)
anchor_h = anchor_h.repeat(batch_size, 1).repeat(1, 1, input_height * input_width).view(h.shape)

这是最后的调整了：

1
2
3
4
5
6
# 计算调整后的先验框中心与宽高
pred_boxes = FloatTensor(prediction[..., :4].shape)
pred_boxes[..., 0] = x.data + grid_x
pred_boxes[..., 1] = y.data + grid_y
pred_boxes[..., 2] = torch.exp(w.data) * anchor_w
pred_boxes[..., 3] = torch.exp(h.data) * anchor_h

之前我们获得的先验框中心是一个0到1之间的数字，加上网格的次序就可以直接检查出是哪个网格中的中心。

结尾：

1
2
3
4
# 用于将输出调整为相对于416x416的大小
_scale = torch.Tensor([stride_w, stride_h] * 2).type(FloatTensor)
output = torch.cat((pred_boxes.view(batch_size, -1, 4) * _scale,conf.view(batch_size, -1, 1), pred_cls.view(batch_size, -1, self.num_classes)), -1)
return output.data

参考：

https://blog.csdn.net/weixin_44791964/article/details/105310627

https://www.bilibili.com/video/BV1Hp4y1y788