卷积双目匹配

双目立体系统中，匹配算法是必不可少的一个环节，但是当今的双目匹配算法效率并不是非常的理想，我在原有的匹配算法中改进了一种算法，并这种算法甚至可以自成一套体系，我称它为卷积双目匹配。

接下来我会介绍我的算法原理，我的算法步骤主要分成以下几步：

• 图像相对滑动
• 图像整体差值
• 通过卷积来计算损失矩阵
• 从损失矩阵中查找最合适的视差值

我会使用下面的两幅图片来进行分析：

两张图片的特点

当左右摆放的相机时，同一个物体在两张图片上的位置会有一个特点：右图片的物体会普遍靠左，左图片物体会靠右。这个现象很容易说明，左相机会照的左面东西多一点，右相机会照右边多一点。

例如，下图中红色矩形标记的桌角，左图桌角的坐标为（200，190），右图桌角的坐标为（167，190），两张图片的桌角的行坐标为是相同的，都是第190行，但列坐标就不同了，而且左图的列坐标为第200列，右图的列坐标为第167列，很明显左图中桌角和右图中桌角相比较更偏右一点。

这个特点会体现在两张图片中所有的物体上，而且，如果这个物体非常靠近相机，这种特点就越明显。在接下来的过程中我会用到这个特点进行处理。

图像相对滑动

利用以上两张图片的特点，我们可以得出一个结论：如果两张图都有一个物体，按照左图这个物体坐标的位置，在右图的这个位置向右寻找，一定能找到左图中相同的物体。

这样就可以建立一个新的方法匹配这些相同的地方。如图所示，先将两张图片完整重叠在一起，然后让右图片进行向右滑动，在滑动的过程中，一定会有一些物体会大概重合，就例如图中桌角的情况。

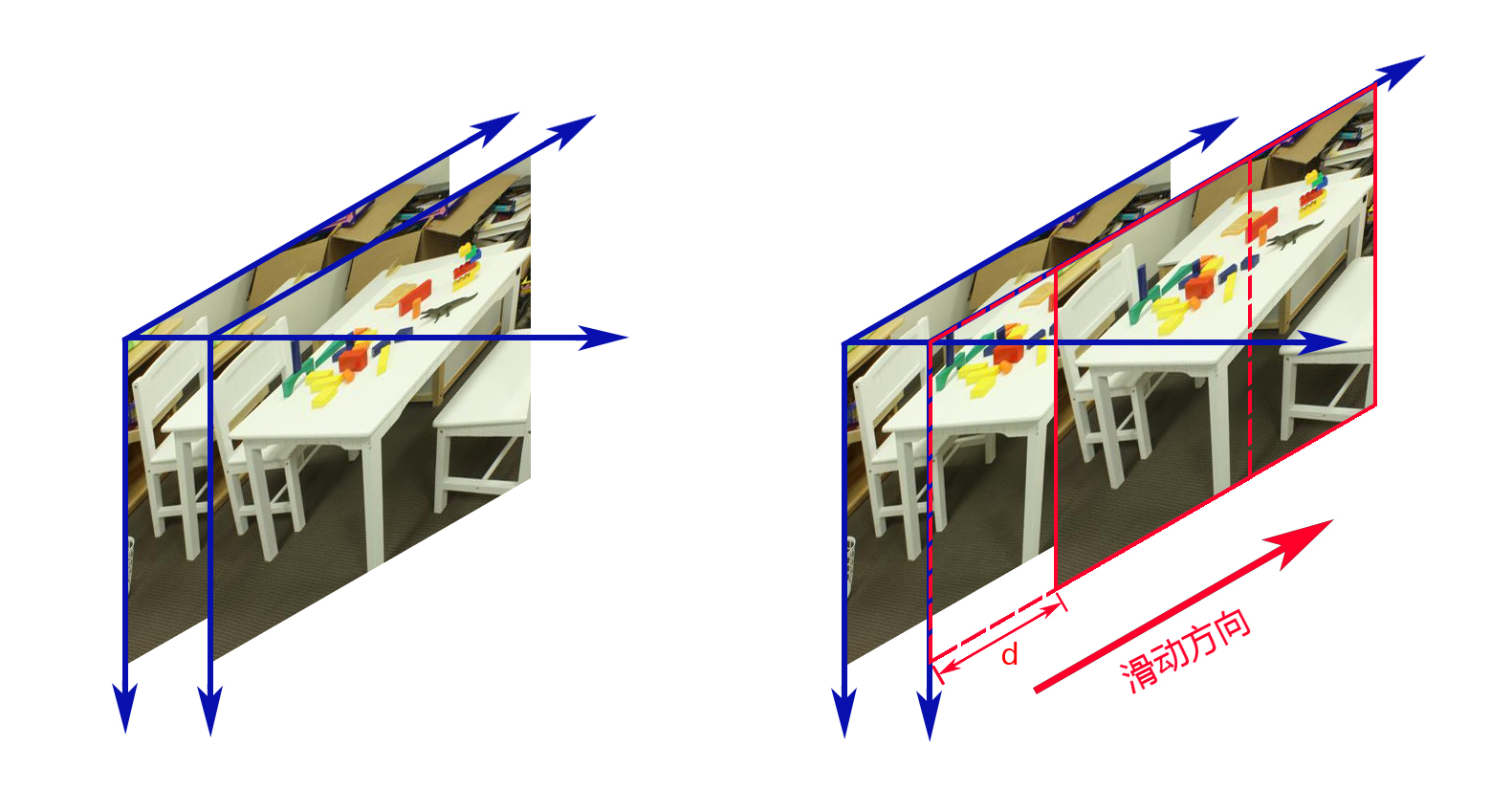
每滑动一次就是移动了一个像素，当滑动了$d$个像素，让一个物体部分区域重合的时候，我们可以认为$d$就是当前像素的视差。

但两张图片不会一直滑动下去，因为没必要，视差值会小于等于整张图片宽度，而等于的情况几乎没有可能，因为一旦等于就意味着物体太靠近相机，导致出现拍摄不全的情况，所以在滑动的时候确定需要滑动多少，太小的话会影响较大的视差部分，太大会加大计算负担，整体时间会增加。我所选的这两张图我预设50次滑动。

图像整体差值

大概的方法已经确定下来了，但现在的问题是如何能确定是否某个区域图片已经重合，这里我是使用了减法操作。

两张图片由于相对滑动，所以可以将重合部分进行相减，而在写程序的时候，可以将左图片的“头部”和右图片的“尾部”去掉就可以保证剩下了重合部分，如图所示。

在两张图片重叠的部分进行相减，会得到一个差值矩阵，当两个区域像素值非常接近的时候，进行减法后得到的数值的绝对值会非常的小，因此通过这个矩阵可以观察出，当前滑动$d$像素下哪些区域非常的接近。

例如，下图是一个模拟出的差值矩阵，若将区域设置成$5*5$，为了进一步比较，将区域A和区域B的数据累加在一起，A区域的累加为24，B区域累加为488，这样说明A区域比较接近，B区域就不太接近，所以A区域更适合当前的视差值$d$（滑动的像素值）。

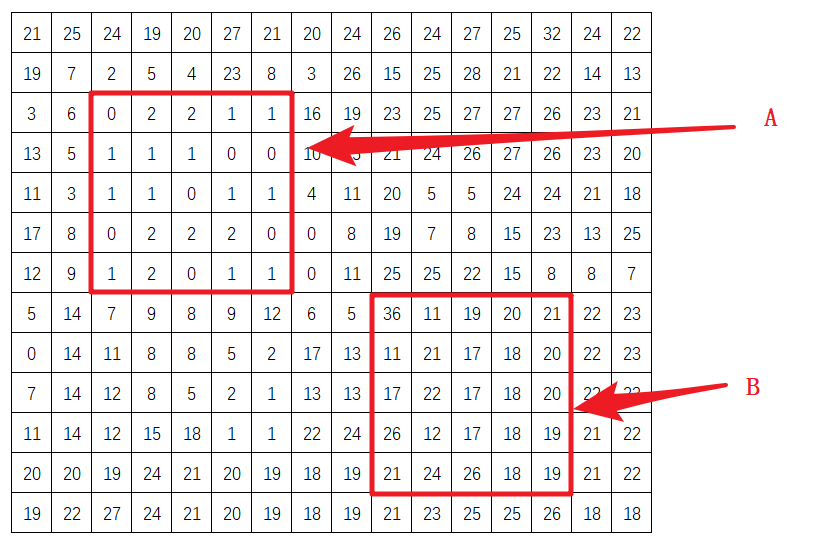
所以每次滑动图片，需要计算差值矩阵，差值矩阵计算完后，需要划分区域，每个区域的元素需要累加在一起得到一个值，由于一整张图片会有很多区域，每个区域可以排布成一个新的矩阵，暂时称之为损失矩阵。

python程序

• 裁剪图片函数

# 裁剪图片函数
def imageCut(image, step):
    """
    image: 需要裁剪的图片
    step: 去掉的宽度（有正负之分）
    
    return: 已经裁剪的图片
    """
    if step < 0:
        # step是负数，去掉图片“尾部”
        image = image[:,:step]

    elif step > 0:
        # step是正数，去掉图片“头部”
        image = image[:,step:]

    else:
        # step为0，图片原封不动
        image = image

    return image

• 计算一次差值矩阵

# 计算一次差值矩阵
def imageDiff(image_right, image_left, step):
    """
    image_right: 右相机图片原图
    image_left: 左相机图片原图
    step: 滑动的像素值
    
    return: 差值矩阵
    """
    
    # 需要改成int16类型，原因如下：
    # 1.无符号类型相减完之后，负数会变成0，所以需要保留负数
    # 2.8位有符号不够用，因为加上了符号位，会丢失最高位的信息
    image_left = image_left.astype(np.int16)
    image_right = image_right.astype(np.int16)

    # 左右图片进行“去头”和“去尾”裁剪
    image1_cut = imageCut(image_left, step)
    image2_cut = imageCut(image_right, -step)

    # 图片相减再取绝对值，即为差值矩阵
    image_cut = np.abs(image1_cut - image2_cut)

    return image_cut

通过卷积来计算损失矩阵

卷积运算在信号中非常常用，同时在图像处理中也有很重要作用。卷积运算需要一个 2 维数据和一个卷积核进行运算。

卷积为如下过程：卷积核旋转180度，但在大多情况下，卷积核是中心对称结构，所以卷积核旋转180度不会影响最后结果。卷积核相当于一个权重的集合，将卷积核在 一个2 维输入数据上进行滑动，根据对准的位置求出所有的加权和，如图所示为其中一种滑动情况。

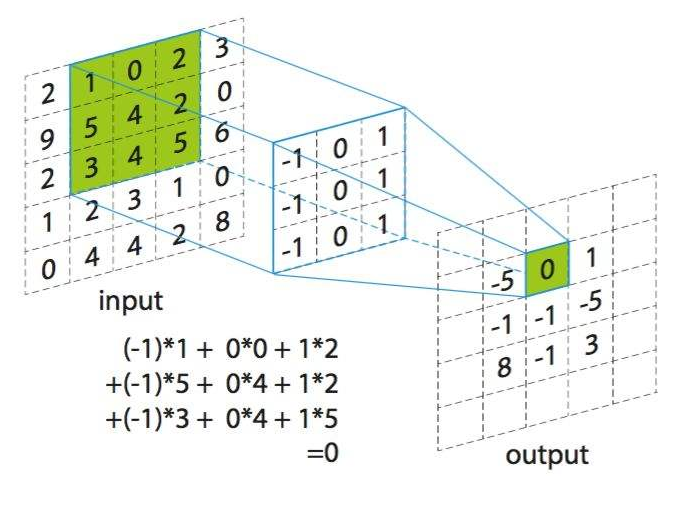
下图为卷积运算的全过程。

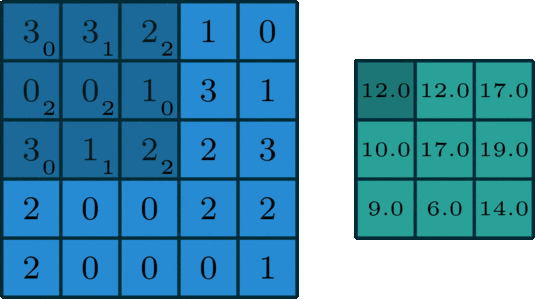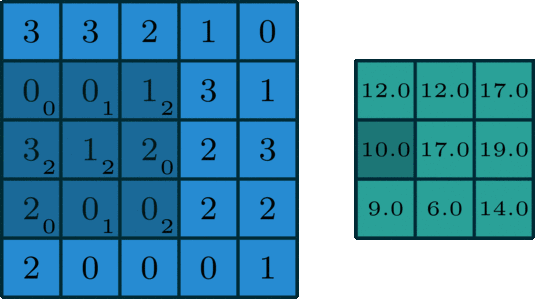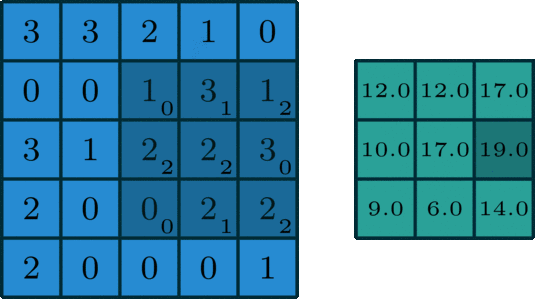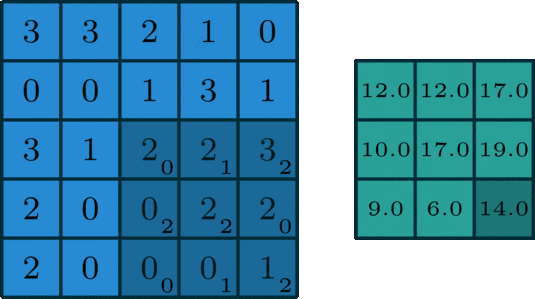
不同的卷积核会产生不同的效果，在这里就不过多介绍卷积核的类型，接下来用到的卷积核是全1矩阵。

这种全是1的矩阵可以将每个区域的所有元素进行累加，这正符合目前的需求，每一次滑动可以说是一次计算当前区域的损失值，只需要一个卷积计算就可以直接出所有区域的损失值，。

这里巧妙利用了卷积的特点，灵感来自于一款卷积神经网络的论文，详细内容直接看我所提供的链接:

OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks

当然也可以看下面这张图，那篇文章中对我比较重要的部分。

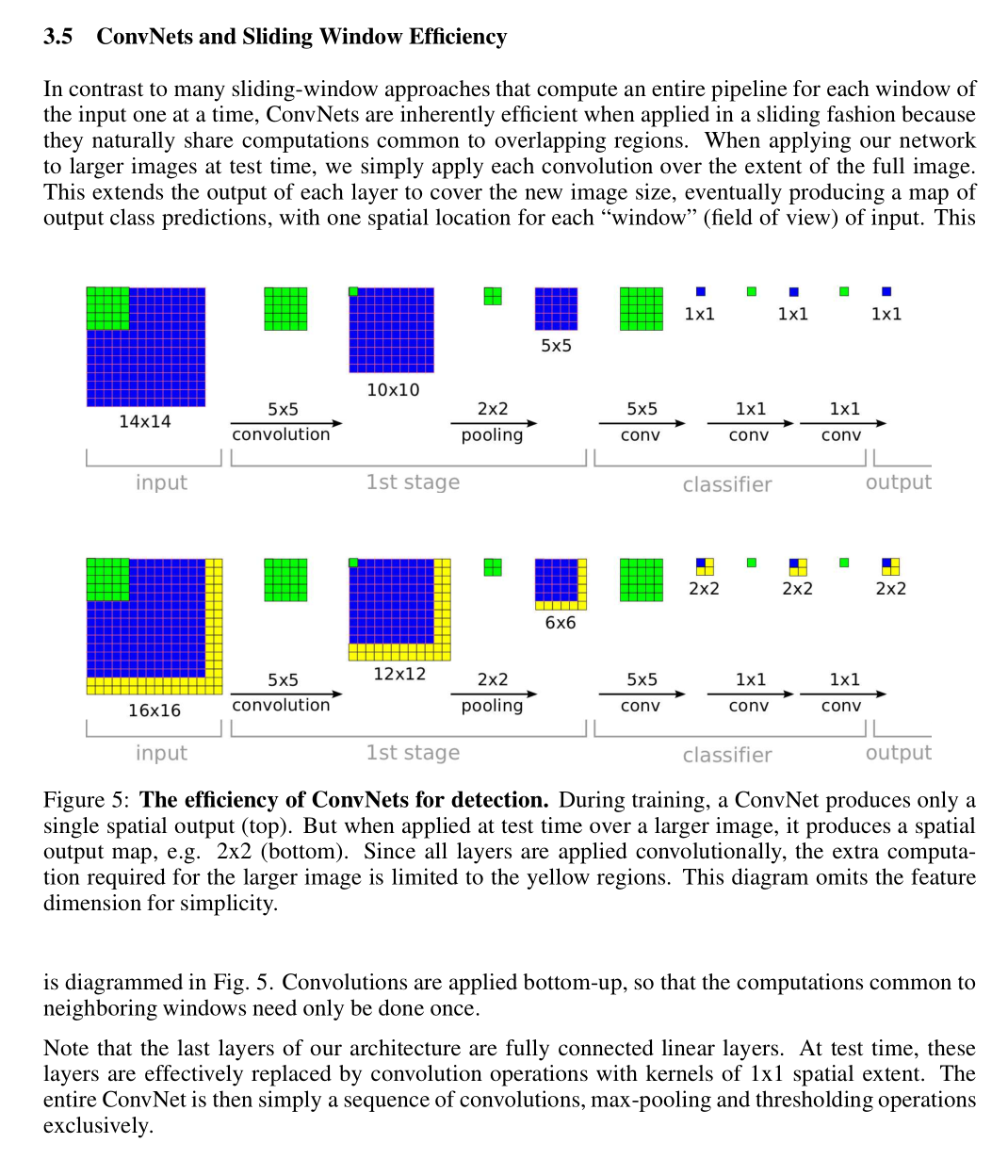
由于每次图片相对滑动都可以获得一个差值矩阵，所以经过卷积后，同样还可以获得一个损失矩阵，由于我预设了50次滑动，所以会得到50个损失矩阵。

python程序

• 计算损失矩阵

def makeImageCost(image_right, image_left, step, core_size):
    """
    image_right: 右相机图片原图
    image_left: 左相机图片原图
    step: 滑动的像素值
    core_size: 卷积核尺寸
    
    return: 损失矩阵（不完整）
    """

	# 调用计算差值矩阵函数，得到差值矩阵
    diff = imageDiff(image_right,image_left, step)

    # 制作卷积核，尺寸为 core_size * core_size 大小的全1矩阵
    core = makeCore(core_size)

    # 通过卷积计算损失矩阵
    cost = myConv(diff, core)

    return cost

从损失矩阵中查找最合适的视差值

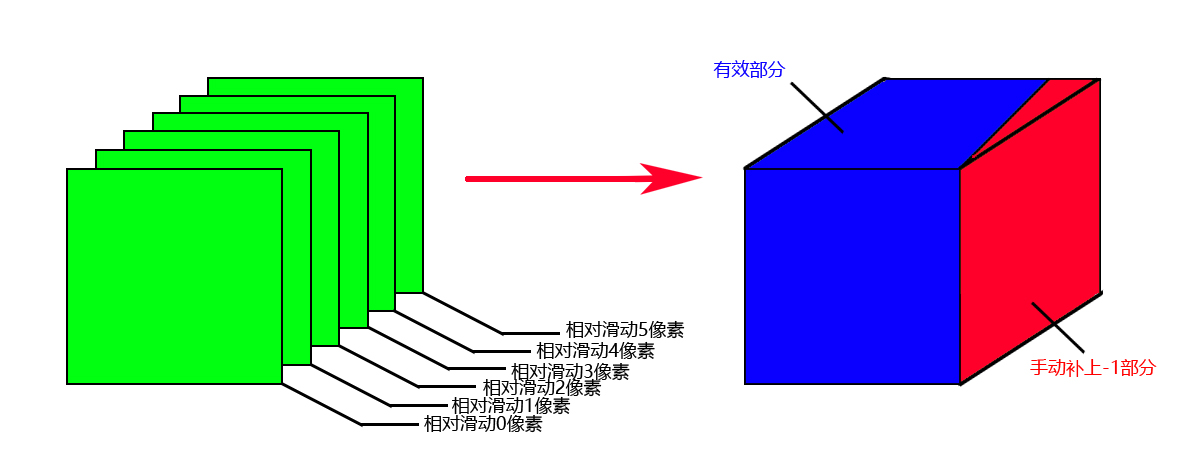
目前为止，根据图片滑动50次，已经计算出了50个损失矩阵，但由于相对滑动，重叠的部分越来越小，50个矩阵的宽度并不相同，只有矩阵的行数相同。为了保持所有的损失矩阵宽度相同，需要把矩阵缺失的部分手动补上。由此可见补上的部分会越来越大，补上的部分每次都会增加一个像素宽度，直到滑动结束。

损失矩阵有个特点，由于卷积前所有值取绝对值，即使经过卷积，所有的值都是正数，为了方便区分补上的部分，补上的值可以使用-1，这样可以保证正数部分是有效的损失。

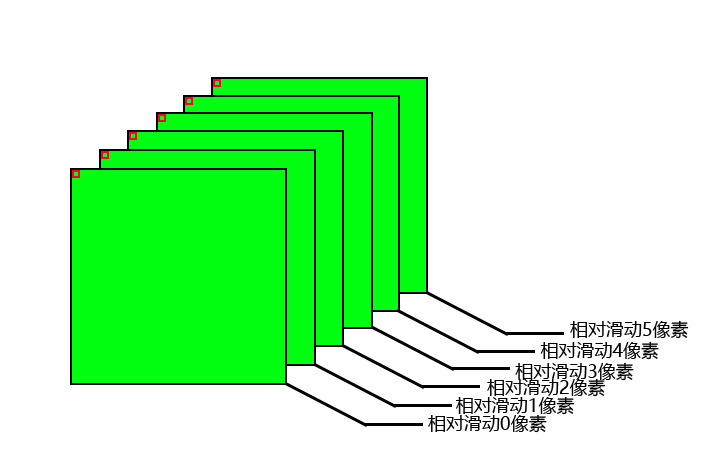
有了50个相同大小的矩阵后，将它们排列起来，没有滑动的损失矩阵放在最前面，接着后面是滑动1个像素的损失矩阵，以此类推，滑动第49个像素的损失矩阵放在最后，这就形成了一个立方体的三维矩阵。

现在就可以检查同50个损失矩阵中的相同位置的大小，其本质是比较一个三维矩阵的第三个维度上的的最小值，在最小值所处的滑动次数，就是该像素的视差值。

例如，如图所示，比较50个损失矩阵最左上角的大小，假设第3个损失矩阵（滑动3像素）的左上角值最小，左上角的视差值为3。

由于之前做过添加-1的处理，所以写程序的时候结合-1的特殊，可以跳过-1的部分，直接找出非负数中最小的值。

通过查找所有损失矩阵最小的损失之后会形成一张新的图，该图为最终视差图。

python程序

• 补上损失矩阵缺失部分

# 补上损失矩阵缺失部分
def makeCostMatrix(image_cost,step, temp):
    """
    image_cost: 损失矩阵（不完整）
    step: 滑动像素值
    temp: 补上的数值
    return: 损失矩阵（完整）
    """

    # 测量出损失矩阵的行数
    image_h = image_cost.shape[0]

    # 先制作一个全1矩阵
    # 全1矩阵乘上一个数，这个矩阵会变成全是这个数
    tem_matrix = np.ones((image_h,step), dtype=np.int16) * temp

    # 合并
    image_step = np.hstack((image_cost , tem_matrix))

    return image_step

• 计算视差图

# 计算视差图
def computParallax(right_img,left_img,N = 30, core_size = 5):
    """
    right_img: 右相机图片原图
    left_img: 左相机图片原图
    N: 迭代次数（相对滑动次数）
    core_size: 卷积核的尺寸，默认是5，建议调大一点
    
    return: 视差图
    """

    for i in range(N): 

        # 计算出不完整的损失矩阵
        img_cost = makeImageCost(right_img,left_img,i,core_size)
        
        # 补上缺失的部分，损失矩阵变得完整
        # 我并没有补上-1，我补上的是一个很大的值，比图片宽度还大
        # 这样在比较大小的时候，省去了排除补上数值的工作
        # 可以直接比较大小，找到最小值
        number = right_img.shape[1] + 1
        image_step = makeCostMatrix(img_cost,i,number)

        if i == 0:
            # 0的情况下，损失矩阵立方体只是一个二维矩阵
            num_matix = image_step
        else:
            # 不断往后面放二维矩阵，最终形成损失矩阵立方体
            num_matix = np.dstack((num_matix,image_step))
            
    # 在损失矩阵立方体的第三个维度上找到最小值
    # 这个值的索引为视差
    min_cost = np.argmin(num_matix, axis=2).astype(np.uint8)

    return min_cost

• 剩下的程序

# 用opencv显示图片
def imageShow(image,second = 0):
    cv2.imshow("image",image)
    if cv2.waitKey(second) & 0xFF == 0x20:
        cv2.destroyAllWindows()

if __name__ == "__main__":

    # 图片路径
    Path_left  = "img\\left.jpg"
    Path_right = "img\\right.jpg"

    # 获取图片
    left_img  = cv2.imread(Path_left,0)
    right_img = cv2.imread(Path_right,0)
   
    # 计算视差图
    min_cost = computParallax(right_img,left_img,N = 30, core_size = 15)

    # 显示视差图，视差值太小了，乘个5清楚一些
    imageShow(min_cost * 5)
    
    # 保存图片
    cv2.imwrite('img.png',min_cost)