本篇文章主要针对于机器视觉常用的坐标系的介绍以及推演，坐标系一共有四种：世界坐标系、相机坐标系、像素坐标系、图像坐标系。除了一些计算过程，还有一部分代码示例。

坐标系简介

注：本篇文章中四种坐标系都是左手坐标系，有些时候比如matlab所使用的就是右手坐标系，这个不会有太大的影响

axis

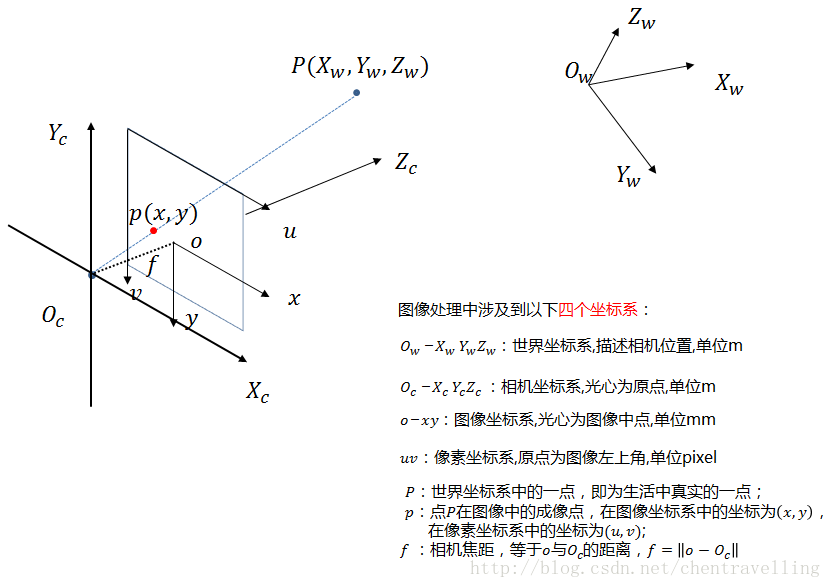
世界坐标系

  • 庞大世界中的坐标系，可以表示万物的位置
  • 单位：m
  • 一般表述相机位置和实物位置
  • Ow-XwYwZw来表示
  • Ow是原点，双目系统中可以将任意一个摄像头的光心设置成原点，即世界坐标系和相机坐标系重合

相机坐标系

  • 存在于相机成像原理上，方便光的直线传播
  • 单位：m
  • Oc-XcYcZc来表示
  • Oc是原点，相机光心的位置，所有光都汇聚这一点

像素坐标系

  • 一张图片中的每个像素位置
  • UV表示，但实际上有第三个坐标轴，用来表示颜色程度
  • 原点在左上角

图像坐标系

  • O-XY来表示
  • 原点位于光轴上的一个点，用物理单位表示像素的位置

变换

世界坐标到相机坐标系

旋转

cri

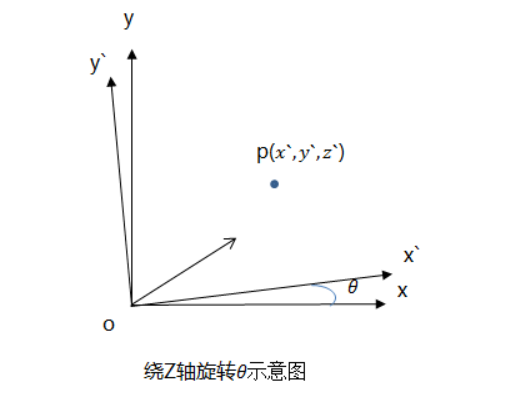
z轴是被围绕旋转的轴，z上的坐标保持不变。

图片为o-x’y’z’旋转成o-xyz的过程

写成矩阵形式：

于是旋转矩阵可以表示为三个矩阵相乘：

  • 这里我们讨论一下旋转矩阵的一些性质：
    • 三个旋转矩阵都是满秩（代数余子式可以算出旋转矩阵的行列式永远为1，也就是永远不会等于零）。
    • 没有旋转的时候就变成了单位矩阵。

平移

平移只需要在一个坐标基础上直接加上偏移量就可以实现平移：

综合到坐标系转换

由此可以推广到世界坐标系乘上一个旋转矩阵，转换成和相机坐标系相同方向的新坐标系，但需要一个平移T将坐标系平移过去：

但上面的公式比较麻烦，写成下面的方式：

  • R为旋转矩阵，（3*3）
  • T为偏移向量，（3*1）
  • 零向量为（1*3）

其实，我不喜欢这种形式，这种形式为了追求规整，放弃了一些比较好的特性，这个主要看个人习惯。我在接下来使用的时候为了计算方便，会再次拆开。

相机坐标系到图像坐标系

两种坐标系存在透视关系，是一种从3D转换到2D的转换，其中可以使用相似三角形进行比例计算。

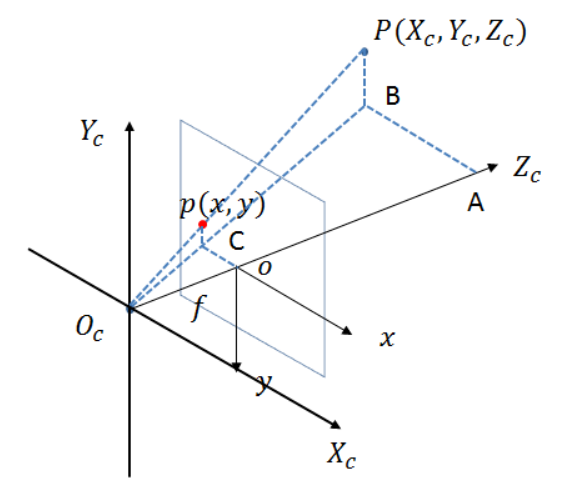
cam2pic

图中有两个相似三角形：

从两个相似三角形中可以找到一些长度的关系：

其中有些可以用其他表示：

于是重新更改一下就变成了新的式子：

我们的目的是想表示出图像坐标系，也就是用其他变量去表示(x,y)，这个时候就可以进行简单修改：

接下来就转换成矩阵形式

图像坐标系到像素坐标系

两个坐标系之间不存在旋转变换，只是原点坐标会有所差距而已

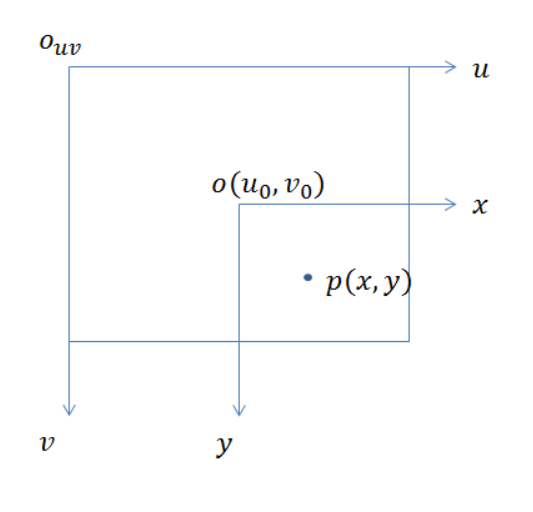
pic2uv

这里假设每一个像素在u轴和v轴方向上的物理尺寸为dx和dy，可以表示为：

写成矩阵形式为：

综合四种坐标系的相互变换

整合

之前讨论了每两个坐标系之间都有一套变换的方法，接下来就可以把这些方法全部综合在一起，生成一个比较复杂的公式，这个公式所表达的意思就是世界坐标和像素坐标的相互转化。

all

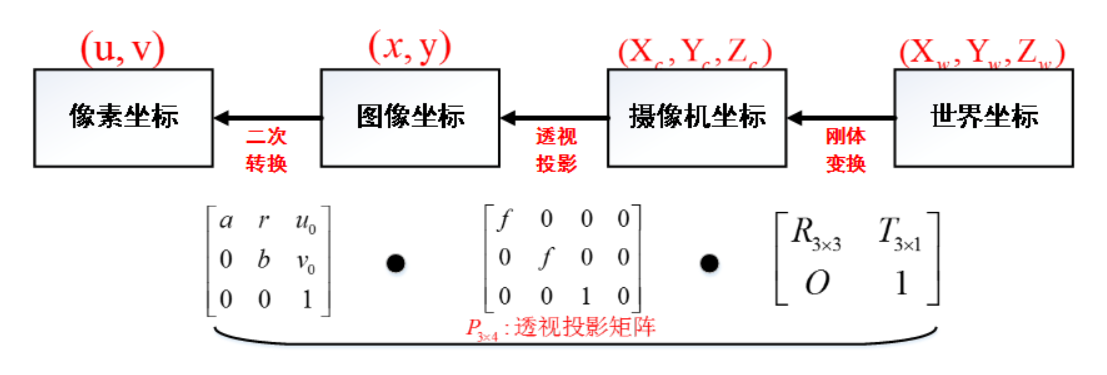
用矩阵公式表达：

接下来我们重新定义一组数据：

以上定义的两数据并没有太大的物理意义，仅仅是因为书写简单方便观看。既然有这种定义式了，那么矩阵中有些地方可以进行相乘，进一步简化：

公式中我分成了两部分，一个矩阵作为相机外参，另一个矩阵作为相机内参：

  • 相机内参：

    这个涉及到相机的构造，有些摄像头买来后，直接去测焦距像素大小可能会很麻烦，而且还不准确，所以这个矩阵一般不会用公式推导求出，这里建议采用张正友标定获取，在matlab中提供了这个程序，只要拍摄几张图片就可以直接获取相机内参。

    注意：matlab中的世界坐标轴有点不太一样，使用的是世界右手坐标系，所以把y轴方向变成了反向

  • 相机外参：

    这个矩阵是描述相机位置，例如在双目系统中，将一个摄像头光心设置成世界坐标系原点时，另一个摄像头可以根据原点进行一个变换，形成了一个新的坐标。

但我并不喜欢以上公式，整个公式是一步一步推理出来的，有几个地方反而有些冗余，我按照我自己的想法稍微修改了一点：

我去点了相机内参中的最后一列和相机外参中最后一行，因为在整体计算中并没有什么作用，以上两个公式都可以使用，主要是怎么方便就用哪个公式去写代码。

如果还想再简化一下，就可以写成这样：

这里的C是一个3*4的矩阵，简化成这样，里面具体的元素已经没有太大的物理含义了，但这样书写有个好处，提前计算出C之后就可以直接使用C来计算整个算式。

通过以上公式，很容易做到三维空间中的一个点在图像中的像素坐标，但反过来就，通过图像中的一个点找到它在三维中对应的点就很成了一个问题，因为我们并不知道等式左边的Zc的值。

像素和世界的相互转换

  • 注：接下来的操作一定要知道深度（Zc或Zw）才能进行，虽然我们目的是求深度，但不影响我们使用下面的几个公式：

像素坐标转换成世界坐标

我把公式(3)改一下：

仅仅是把Zc移到了右边，其实如果世界坐标和相机坐标系重合的话，Zc=Zw。

整个函数的意思是，如果我们知道了世界坐标中具体的某一点坐标三个数值，就可以直接带入，求出u,v。

世界坐标转换成像素坐标

这时候我们不能去用公式(3)去修改，我们可以换个思路，使用公式(2)去修改：

由于公式(2)中的相机内参是一个3*3的对角矩阵，而且很明显是一个可逆矩阵（对角中不会出现0），那么就可以求出这个矩阵的逆矩阵，写成以下形式：

简单计算一下，等号左边最后计算的结果是一个3*1的矩阵，右边部分我们换个思路，回想一下外参矩阵的推演过程，我们可以写成这样：

那么所有矩阵往左边移动：

虽然在双目系统中，我们做不到提前给出Zc或Zw，所以以上公式进行参考即可，在一定程度上还是比较方便。

程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
import numpy as np
import scipy.io as sio

class CameraMatrix:
	def __init__(self, path = 'camera_data.mat'):
        
		# 从camera_data.mat文件中导入数据
		data=sio.loadmat(path)

		self.leftInsideMatrix = data['leftInsideMatrix']
		self.rightInsideMatrix = data['rightInsideMatrix']
		self.leftOutsideMatrix = data['leftOutsideMatrix']
		self.rightOutsideMatrix = data['rightOutsideMatrix']

		self.__dataInit()

	def __dataInit(self):

		# 分解出旋转矩阵
		self.left_R  = self.leftOutsideMatrix[:3,:3]
		self.right_R = self.rightOutsideMatrix[:3,:3]

		# 分解出偏移向量
		self.left_T  = self.leftOutsideMatrix[:3,-1:]
		self.right_T = self.rightOutsideMatrix[:3,-1:]

		o = np.array([0,0,0]).reshape(-1,1)

		# 制作出规整的相机内参
		leftInsideMatrix  = np.concatenate((self.leftInsideMatrix,o),axis=1)
		rightInsideMatrix = np.concatenate((self.rightInsideMatrix,o),axis=1)

		# 计算出完整相机参数
		self.leftCameraMatrix = np.dot(leftInsideMatrix, self.leftOutsideMatrix)
		self.rightCameraMatrix = np.dot(rightInsideMatrix, self.rightOutsideMatrix)

		# 计算出相机内参的逆矩阵
		self.leftInsideMatrix_T_  = np.linalg.inv(self.leftInsideMatrix)
		self.rightInsideMatrix_T_ = np.linalg.inv(self.rightInsideMatrix)

		# 计算出旋转矩阵的逆矩阵
		self.left_R_T_  = np.linalg.inv(self.left_R)
		self.right_R_T_ = np.linalg.inv(self.right_R)

	def countPic(self,x_w,y_w,z_w,cam = 'l'):
		# 通过世界坐标计算出图像中像素坐标
		# （x_w,y_w,z_w）坐标
		
		if cam == 'l':
			ma = self.leftCameraMatrix

		elif cam == 'r':
			ma = self.rightCameraMatrix

		w_xyz  = np.array([x_w,y_w,z_w,1]).reshape(-1,1)
		p_uv = np.dot(ma,w_xyz) / z_w

		return int(p_uv[0,0]),int(p_uv[1,0])

	def countWord(self,u,v,z_w,cam = 'l'):
		# 通过像素和深度计算世界坐标
		# 第u行v列像素

		if cam == 'l':
			ma = self.leftInsideMatrix_T_
			R_T_ = self.left_R_T_
			T = self.left_T

		elif cam == 'r':
			ma = self.rightInsideMatrix_T_
			R_T_ = self.right_R_T_
			T = self.right_T

		p_xyz  = np.array([u,v,1]).reshape(-1,1) * z_w

		# 公式计算

		w_xyz = np.dot(R_T_,(np.dot(ma,p_xyz) - T))

		return w_xyz[0,0],w_xyz[1,0],w_xyz[2,0]

if __name__ =="__main__":

	c = CameraMatrix()
	print(c.countPic(55,56,29))
	print(c.countWord(1227, 1206,29))